In high school, you almost never see a “real” proof. You only see those Statement/Reason proofs in Geometry. These types of proofs never really show you what real math proofs are really like. So, here are 2 for you:
Category: Algebra
RE: Birthday Dinner
Yes, life does go by fast. Strangely, the older you get, the faster it goes. I do not know why this is.
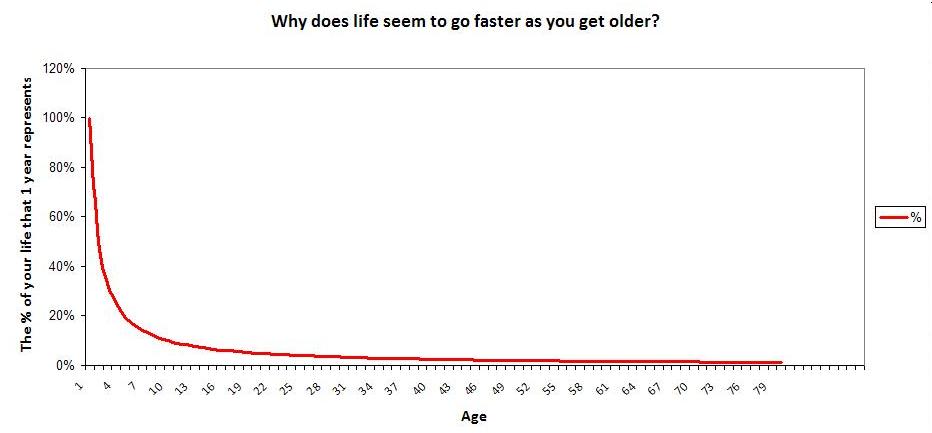
Ever get an email like this? Well, as your age varies, the percentage of your life that a single calendar year represents also varies. As you get older, a year is a smaller percentage of your overall life. In other words, 1 year represents 50% of a 2 year old’s life. However, it is only 2% of a 50 year old’s life. So, perhaps that is why each year seems to go by faster.
Want to see the percentage for every age from 0 to 80? Let’s make a formula and graph it. The percentage of your life that a single year represents is just a function of your age: \(f(age) = \frac{1}{age}\) If you graph this on a spreadsheet, you’ll get the following:
How would you interpret this graph? You’ll notice that once you pass the inflection point, the percentage seems to flatten out. So, at what point can a person legitimately start saying “Wow, this year really flew by?” Based on the graph, teenagers might feel this almost as much as middle aged people.
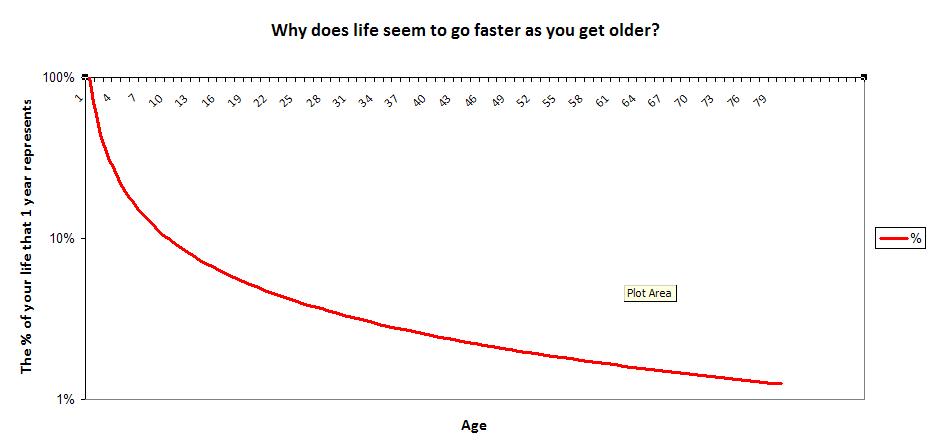
Lastly, do you notice how scaling of the y-axis makes the difference between age 15 and 50 look trivial? In order to properly display percentage changes, I will scale the y-axis logarithmically. Here is the result:
With this scaling, you can see a year in the life of a teenager (~6%) is quite different than a year in the life of someone in their 50s (~2%)
Optimal Snowboard Length Formula
http://www.livestrong.com/article/87496-size-snowboards/
Evaluate your height. This is the best way to determine snowboard length. One typical formula used by professional snowboards is: rider height (in inches) x 2.54 x 0.88 = suggested snowboard length. This will help you to start narrowing down your snowboard choices.
When I saw this formula, I wondered what it meant. Note that snowboards are measured in centimeter units. Well, to convert inches to centimeters, you multiply by 2.54. So, we’re converting height to centimeters and then taking 88% of that. I have no idea where the 88% rule comes from. The point being, the “formula” is just saying to get a snowboard that is 88% of your height. This lines up with my mouth, and I am pretty sure I am well-proportioned. So, maybe it’s just easier to say that a snowboard should come up to your mouth.
This is also an example of intentionally not simplifying an expression because you lose some inherent meaning (explicit unit conversion, etc). Otherwise, the equation could be simplified to length = 2.235 * rider height (in inches)
In a room full of men, ¾ of them are married.
There are 6 more married men then unmarried.
How many married men are there?
Set up the equations…
In manufacturing/engineering, there is a concept known as the bathtub curve. In theory, something that is brand new (including a human being!) is more likely to have failures than something that is a little older and has worked out those early kinks. Of course, once the product gets old, you’ll start having new reasons for failure (things wearing out).
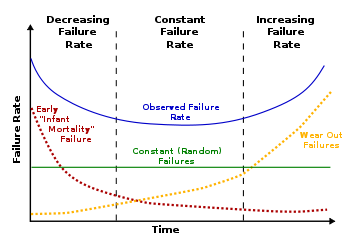
I don’t have much to add on this topic, but I created this post this for two simple reasons:
- First, it’s a nice example of a Cartesian graph that makes intuitive sense. The aggregate blue curve indicates that new things can be lemons, then they work smoothly, and then they wear out and start breaking again.
- Also, I think its a great example of an authentic real-life piecewise function. As you can see, it has three very different sections.
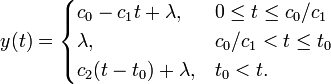
Question: In terms of cars, do you think the blue curve above would be so symmetric?