I noticed a for sale ad for a 1996 Mustang, and was struck by the $3500 price… ’94-‘04 Mustangs seem like a great bang for the buck: They are cheap, plentiful, have lots of parts available, and there’s lots of online DIY support. Perfect for a student or hobbyist on a budget.
I opened up 35 ads and noticed 19 were manual. I realized I was staring at a confidence interval problem!
Is this bad science? Since this is a retrospective study, there is non-random assignment for the treatment and control groups. That introduces selection bias. Projects that are more likely to implement a (long-winded) “waterfall” life-cycle approach are probably larger scale projects to begin with. Correlation is not causation. So, maybe it’s not the lifecycle approach that is the problem, but the confounding/lurking variable of project scale that is the problem. The study should control for the size of the project to make a valid conclusion about success rate of the development approach used. ie: Building a large insurance processing system will use a lifecycle approach, while building a fitness app will not. Apples to oranges, since one is much easier to be implement than the other.
At least they tried to control for 1 variable. They controlled for happiness level prior to the marriage, which has nothing to do with happiness while married. But, this study is still rubbish due to survivorship bias. People who are happy with their marriage will stay in the marriage. People who are unhappy may not stay in the marriage, and are not part of the study. To really measure if marriage causes happiness, you must run a controlled experiment and randomly assign people to a control and treatment group. The results of an observational study are invalid and meaningless. The article should conclude that “People who are in great marriages and decide to stay married …are happier than single people”
Incidentally, the article headline implies “Marriage makes you happy” Meanwhile, they later state the effect of living together makes you just as happy as legal marriage. So, they show that marriage has nothing to do with happiness, yet the headline states the exact opposite. Another case of a headline that the masses just accept at face value.
When comparing test scores of different countries, you need to control for variables. This is basic statistical illiteracy. Vastly different Student income and teacher workload are 2 factors are never mentioneds
Want to close the achievement gap? Close the teaching gap
Here is an example of selection bias. Correlation is not causation. Those with serious illness and poor health will not be in the active group. The limits of an observational study vs. a properly controlled experiment with random assignment.
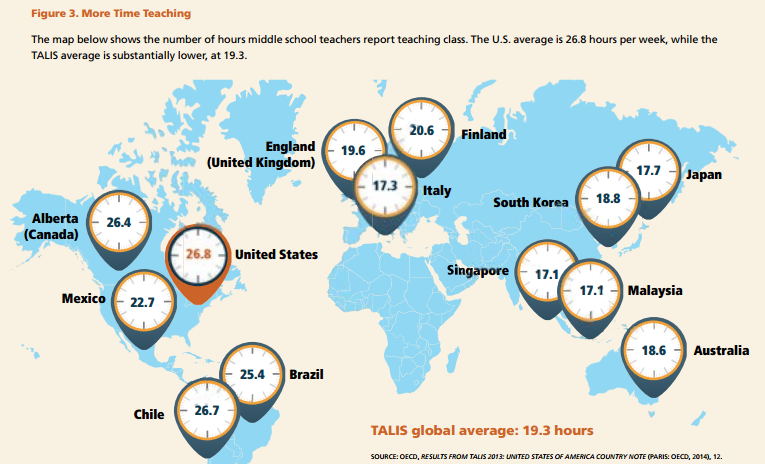
In my dummy sports data below, you can see that the number of penalties is correlated most strongly to wins.
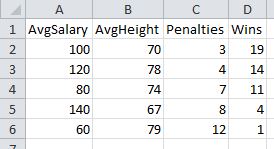
But, if you had hundreds of variables, how could you generate the cross product of every correlation possible, in order to find the variables with the highest correlation? One answer: Use the Stats program called “R” to create a correlation matrix! You can generate all sorts of visual outputs, as well. Penalties sticks out like a sore thumb now:
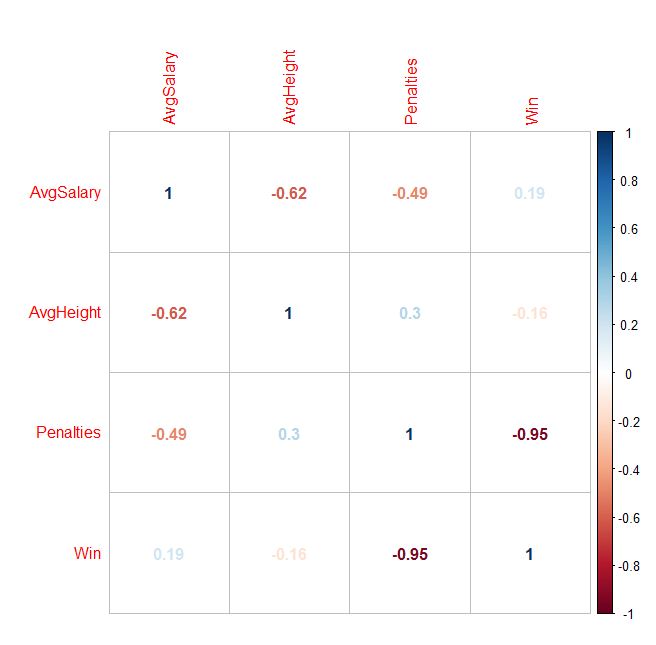
Disclaimer: Without stating a hypothesis up front, these finding is nothing more than “data snooping bias” (ie: curve fitting) The discovered association might simply be natural random variation, which would need to be verified with an out of sample test to have any validity at all.
To do this for yourself, here are the steps:
Enter the following commands in R:
(The lines with # are just comments, do not type them. Just paste the bold commands!
# Import data
> data1 <- read.csv(file.choose(), header=TRUE)
# Attach data to workspace
> attach(data1)
# Compute individual correlations
> cor(Penalties, Win)
# Scatterplot matrix all variables against each other
> pairs(data1)
# Generate a CORRELATION MATRIX !!
> cor(data1)
Here is how to generate the visual output:
> library()
…Scroll back up to the very first line of the popup window. Packages are probably in something like library ‘C:/Program Files/R/R-3.3.0/library’
Download and install “corrplot” Windows binaries package into the library path above.
Note: When you extract, you will see the folder heirarchy: corrplot_0.77/corrplot/….
Only copy the 2nd level folder “corrplot” into the library/ folder. (ie: Ignore the .077 top folder)
# import corrplot library
> library(“corrplot”)
# generate correlations matrix into M
# You now redirect the cor() function output we used above into a matrix called “M”
> M <- cor(data1)
# Plot the matrix using various methods
# Method can equal any of the following: circle, ellipse, number, color, pie
> corrplot(M, method = “circle”)
> corrplot(M, method = “ellipse”)
> corrplot(M, method = “number”)
> corrplot(M, method = “color”)
> corrplot(M, method = “pie”)
Here is a question someone recently asked me: What’s the probability that two students taking a multiple choice test with 29 questions will get exactly the same wrong answers on 10 of the questions?
Krueger and Dale studied what happened to students who were accepted at an Ivy or a similar institution, but chose instead to attend a less sexy, “moderately selective” school. It turned out that such students had, on average, the same income twenty years later as graduates of the elite colleges. Krueger and Dale found that for students bright enough to win admission to a top school, later income “varied little, no matter which type of college they attended.” In other words, the student, not the school, was responsible for the success.
http://www.brookings.edu/research/articles/2004/10/education-easterbrook
- Singapore’s student population does not include the children of huge numbers of people who work the lower-paying jobs in Singapore.
- For Singaporean students, school is their job; other activities are absent or relegated to minor roles.
- Most Singaporean children get additional schooling beyond the school day through individual tutoring or classes. (One survey found 97% of Singaporean students get private Math tutoring)
http://www.nytimes.com/2013/12/22/opinion/sunday/music-and-success.html
I wanted to examine the correlation between a student’s performance in Algebra 2 and his subsequent performance in Trigonometry. This provides an opportunity to see if our past course recommendations were sound. (In this case, the decision to place a student from Algebra 2 into either Trig or a more remedial Math course) I felt this data might be useful in determining a cut-off score for promotion into the next course. ie: Is there a grade threshold in the 1st course that is associated with failure in the 2nd course?
Results: It’s a small sample size (n=25), but the 3 students who scored under 75 (overall) in Algebra 2 ended up failing Trigonometry. The r-squared was .24, which can be interpreted as saying that 49% of the variation in the Trig grades were explained by the Algebra 2 grades.
- The problem is that if you have collected a whole bunch of data and you don’t find anything or at least nothing really interesting and new, no journal is going to publish it.
- So if you, as a researcher, don’t find anything counterintuitive that disconfirms prevailing assumptions, you are usually not even going to bother writing it up.
Rod Carew, one of the few to make a serious run at .400 since Williams, has studied the .406 season and contends that Williams’s absences were a blessing.
“The fewer at-bats any hitter has over the required number of plate appearances, the better his chance is of hitting over .400,” Carew wrote in an e-mail responding to questions about 1941. “When I hit .388 in 1977, I had 694 plate appearances and 616 at-bats (239 hits). Ted had something like 450 at-bats in 1941 when he hit .406, and I think George Brett and Tony Gwynn had fewer then 450 at-bats when they made their runs at .400.
“All in all, the less at-bats, the better.”
He’s trying to articulate the Law of Large Numbers. Anyone hitting near .400 is deviating from the expected proportion of hits. If you flip a coin 10 times, you just might get 7 tails. If you flip if 1000 times, there’s no chance you’ll ever get 700 tails. Many people may bat .400 during a single game (a handful of at-bats), but almost no one does as the number of at-bats increases. Their average converges to the more realistic season average.
…97 percent of all Singaporean students, nearly 90 percent of South Korean primary students and about 85 percent of Hong Kong senior secondary students receive tutoring.
Tutoring Spreads Beyond Asia’s Wealthy
When comparing test scores of various countries, are they comparing similar samples? No. Just one (of many) confounding variable that needs to be controlled for is the amount of private tutoring each group of students receive.
Mr. Pane conducted a study, financed by the federal Department of Education, of an algebra software program. He found that high school students who used the program …showed gains on their state-standardized math tests that were nearly double the gains of a typical year’s worth of growth using a more traditional high school math curriculum.
Double! Well, that sounds impressive. But, you want to know what exactly these “doubled gains” actually are. Does it mean a gain of 2 points instead of 1 point? Or does it mean 30 points instead of 15?
Note the last step in critically evaluating a study or experiment:
So, in light of #7, you should to read the actual study, and not a summarized interpretation in a newspaper. Here are some notable excerpts from the actual study:
So, when you read the fine print, you learn that scores actually go down in the first year, and the improvement may not be as large you the article led you to believe.
This is a great example of a shamelessly biased graph. USA’s cost is grossly exaggerated by extending the bars to include 95th percentile, while none of the others do this. Blatant!
The studies that Flegal did use included many samples of people who were chronically ill, current smokers and elderly, according to Hu. These factors are associated with weight loss and increased mortality.
Here is my favorite part of Leonard Mlodinow’s book “The Drunkard’s Walk: How Randomness Rules” Watch from 5:46