Category: Probability

Categories
Probability Statistics

Cheating on a test?

Here is a question someone recently asked me:  What’s the probability that two students taking a multiple choice test with 29 questions will get exactly the same wrong answers on 10 of the questions?

 

My answer?   Let’s restate this question to make it a lot simpler.  Can we assume they also got the same correct answers?   If so, then the question simply becomes, “What’s the probability that 2 students choose the same answer for all 29 questions?”
P(all same) = \((1/4)^{29} = .000000000000000003\)
Categories
Probability

Why Casinos Don’t Lose Money

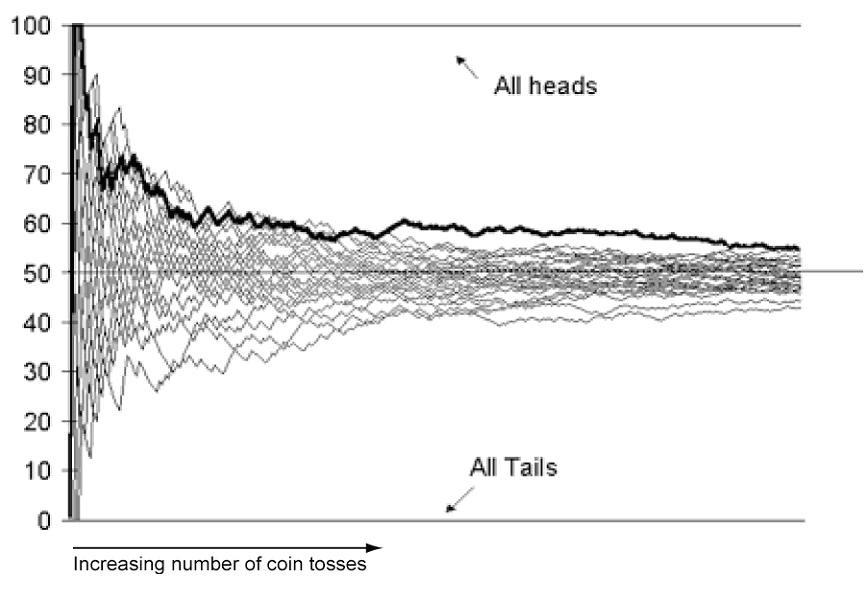
First, let’s illustrate the law of large numbers.  If you flipped a coin 10 times, you should expect to get 50% heads.  However, this may not happen.  You could get anything from 0 to 10 heads.  The most likely outcome is flipping 5 heads, and the odds of this outcome is 50%.  Variations from this become increasingly less probable.  For example, the odds of you flipping 4 or 6 heads is 26%, and the odds of you flipping 3 or 7 heads is 10%.  Now, let’s say you flipped a coin 100 times.  The odds of getting exactly 50% heads is still 50%.  But, do you think the odds of getting 60 heads is also 26%?  It’s actually only 2%.  It’s much easier to get 6 out of 10 heads, than it is to get 60 out of 100 heads.  What are the odds of flipping 600 heads out of 1000 flips?  It’s 0.00000001%.  With 1000 flips, you’re pretty much always going to get around 48%-52% heads.  Deviations beyond that range are very improbable.  So, in summary, the law of large numbers states that the more trials you have, the closer your actual outcome will be to the theoretical expected probability (In this case, the more coins you flip, the more you’ll start to approach actually getting 50% heads)

So, how does this tie into casinos?  Let’s take the roulette wheel as our example.  There are 37 total numbers.  18 reds, 18 blacks, and 1 green.  If you guess red or black correctly, you’ll get a 1:1 payout (ie: If you bet $1, you’ll get back $2, thereby winning $1).  If the wheel lands on green (0), both red and black lose.  This is where the casino gets it’s edge in this particular gamble.  Let’s calculate the expected value of a $1 bet on red.

\(E[X] = \frac{18}{37}(\$1)+\frac{18}{37}(-\$1)+\frac{1}{37}(\$-1) = -\$.03\)

 

What this means is you have an 18/37 chance of winning $1 (if it lands on red), and 18/37 chance of losing $1 (if it lands on black), and a 1/37 chance of losing $1 (if it lands on green)  The expected profit for playing this game is negative 2 cents.  Now, sometimes you’ll win, and sometimes you’ll lose, but if you play enough times, you’ll be averaging a loss of 23 cents per round.  This is where the law of large numbers comes into play.  As long as enough people are playing, the house will be averaging a profit of 2 cents for every dollar bet on that roulette table.

Question: What is the expected value of correctly guessing a specific number? There are 37 numbers, but the payout is 35:1 (You get paid $35 for each dollar you bet)  Based on this answer, is it smarter to try guessing the color or guessing the number?

 

Categories
Probability

Quitting While You’re Ahead? Random Walks & Markov Chains

Question:  What if you walked up to a “fair” casino game (50/50 odds of winning) that pays even odds with $10,000, and said you would quit as soon as you’re up $1,000 ? (ie: You either walk out with $11,000 or keep playing until you lose everything)  What are the odds of you leaving the casino with a $1000 profit?

A Markov Chain can virtually simulate many random walks of this experiment.  With a large enough sample size, you can get an accurate sense of the odds of walking out with $1,000.

The following code runs this simulation as many times as you want, and tells you how many times you got to $11,000.

#!/usr/local/bin/perl
#!/opt/bin/perl

use Getopt::Long;
use strict;

GetOptions("f:s", "debug", "v");

my $current_round = 0;
my $starting_amt = 10;
my $lost = 0;
my $won = 0;
my $current_amt;
my $x;
my $low_bound = 0;
my $high_bound = 11;

while ($current_round < 100) {
while ($current_amt > $low_bound && $current_amt < $high_bound) {

		#generate a 1 or 0
		$x = int(rand(1)+.5);

		#adjust to either +1 or -1
		if ($x == 0) {
			$x = -1;
		}

		# update total
		$current_amt -= $x;

		# print current total
		print "$current_amt ";

	}

	print "\n";

	#increment rounds won or lost...
	if ($current_amt == 0) {
		$lost++;
	} else {
		$won++;
	}

	#reset current amount for next round
	$current_amt = $starting_amt;

	$current_round++;
}

print "\nWon = $won\n";
print "Lost = $lost\n";

Answer:  Doing 100 rounds is a large enough sample size to get an accurate result.  On average,  you’ll walk out with $11,000 about 90% of the time you try this experiment.  Why is this still a bad idea?  In practice, gamblers rarely quit while they are ahead, and you still have that 10% odds of a total washout.  Recall, the expected value of this game is still break even.

Here is a sample output of 10 rounds:

Won = 9
Lost = 1

Continue reading “Quitting While You’re Ahead? Random Walks & Markov Chains”