Mauna Kea on the Big Island of Hawaii is considered to be one of the hardest bicycle climbs in the world. It climbs 13,803 feet over 42 miles from sea level.
How steep is this climb?
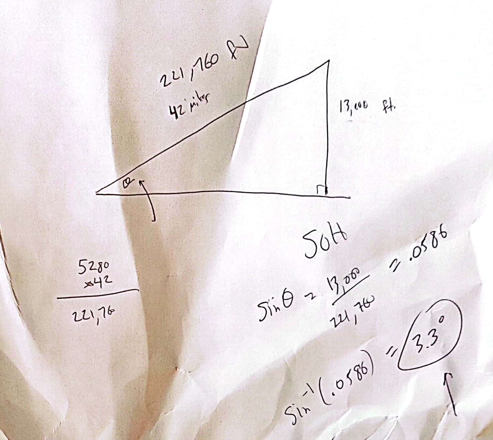
Mauna Kea on the Big Island of Hawaii is considered to be one of the hardest bicycle climbs in the world. It climbs 13,803 feet over 42 miles from sea level.
How steep is this climb?


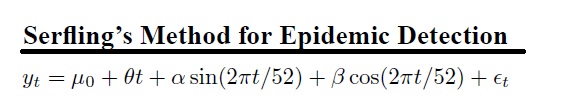
In a nutshell, the sin() and cos() terms are periodic curves, and the weighting of the various coefficients is what allows proper regression fits. Let’s take a closer look at the formula, and try to make sense of it.
For example, as t goes from 0 to 52, \(\frac{t}{52}\) goes from 0 to 1, \(2\pi * \frac{t}{52}\) goes from 0 and 360. (and then it repeats since sin repeats in multiples of \(2\pi\) and therefore \(sin(2\pi * \frac{t}{52})\) goes from sin(0) to sin(360) which is a full periodic cycle of this function. Note the same logic applies to the cos() term in the formula.
The picture says it all.
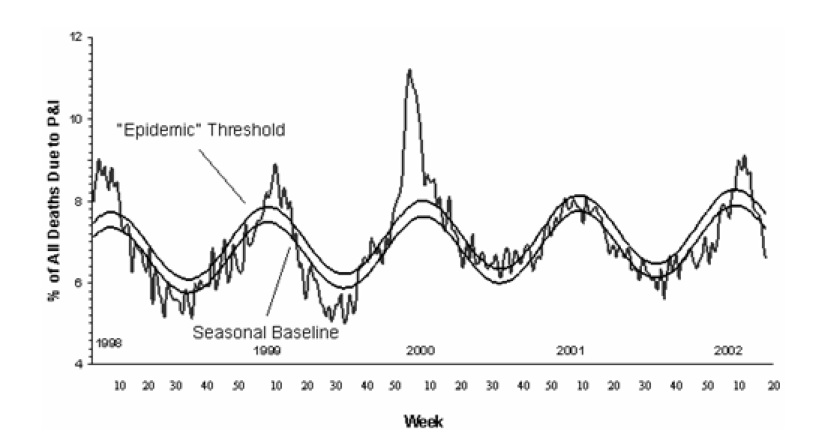
Further Reading: Automated Detection of Influenza Epidemics with Hidden Markov Models
![]()
Wow, a real life formula that uses the double angle trig. identities! As you can see, the distance a projectile will travel is a function of: velocity, gravity, and the launch angle.
First, a quick fraction review: First, recall that \(\frac{1}{1000}\) is a lot smaller than \(\frac{1}{10}\). Conversely, we can also agree that \(\frac{1}{100}\) is a lot smaller than \(\frac{99}{100}\). ie: The bigger the denominator (and/or smaller the numerator), the lower the value of the (positive) fraction.
So, since v is in the numerator, the distance traveled (d) increases directly with velocity (in a big way, since it’s squared) Next, since g is in the denominator, the distance traveled decreases as gravity increases. (Makes sense, right?)
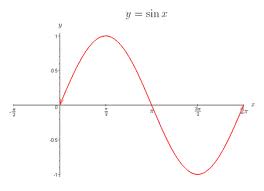
This is a graph of all Sin(x) values from 0 to 360. The x-axis is divided into quadrants (0, 90, 180, 270, 360). Notice in the graph that Sin(x) rises from 0 to 1 as x rises from 0 to 90 degrees. Then, it drops from 1 back to 0 as x rises from 90 to 180 degrees.
Refer back to the double angle \(Sin(2\theta)\) in the original formula up top. So, as x rises from 0 to 45 degrees, 2x actually rises from 0 to 90, and the \(Sin(2\theta)\) value is increasing. But, as x continues to rise from 45 to 90 degrees, 2x rises from 90 to 180, which means the \(Sin(2\theta)\) value is now decreasing.
So, what’s the ideal angle to throw something? The one that maximizes the value of \(Sin(2\theta)\), since it’s a multiplier in the projectile formula. Well, as you can see in the graph, Sin(90) = 1, the highest possible value for Sin(x). So, the ideal launch degree is x = 45 (which puts 2x at 90).
So, now you know why the ideal angle in these video games is 45 degrees, and have an inkling of how programmers create classic games like these: